Taproot 101
By now, anyone interested in the technical aspect of Bitcoin must have heard the name Taproot. What is it?
Taproot is a Bitcoin update activated in November 2021. It is the most anticipated upgrade since SegWit in 2017. Taproot consists of three Bitcoin Improvement Proposals (BIPs), focusing on Schnorr Signature (BIP 340), Taproot (BIP 341), and Taproot Script (BIP 342), respectively. They have collectively improved Bitcoin's scripting capabilities in efficiency, privacy, and flexibility, without adding new security assumptions.
So, have you ever wondered whether these fancy techniques can be applied to other blockchains? The answer is yes, and this post will explain how. These techniques have values beyond their implementations in Bitcoin; with proper adaptations, we can bring their merits to CKB (Common Knowledge Base) blockchain as well.
Before diving into the details, let’s get familiar with Taproot 101 first. For those who are already familiar with Taproot, feel free to skip to the next section.
We assume that you already have some knowledge about ECDSA (Elliptical Curve Digital Signature Algorithm), and you know, for example, what G (generator), elliptic curve, and secp256k1 are. No worries if you don’t, I’ve found a piece here on elliptic curve cryptography. If you spend a few minutes on the foundation first, the later reading will be much easier.
There are two crucial components in Taproot: Schnorr Signature and Merkle Tree. Schnorr Signature is at the heart of Taproot implementation. It was proposed to replace secp256k1 for authenticating transactions. The secp256k1 standard, despite its wide adoption, has several downsides by contrast with Schnorr Signatures in terms of simplicity, security, and non-malleability. A Merkle Tree is an example of a cryptographic commitment scheme capable of partial reveal. There are several Merkle Tree variants but in this post, I’ll only introduce the vanilla Merkle Tree.
Mathematics in Schnorr Signature
Schnorr Signature is produced from the Schnorr signature algorithm, firstly described by Claus-Peter Schnorr back in the 1980s. It was craved and embraced by the blockchain community after the patent expired in 2008. Let's look into the structure of Schnorr Signature to better understand its benefits.
The mathematical conventions used here are:
- Lowercase: scalar
- Uppercase: curve point
- ||: binary concatenation
- Same letter in different cases: letter in lowercase is the X-coordinate of the curve point of the corresponding letter in uppercase. For example,
Calculate: r from R, which means r is the X-coordinate of the curve point R.
The signing of Schnorr Signature is shown below:
Private Key: k
Public Key: P = k * G
Message Hash: m
--- the above are already given ---
Generate a random number: z
Calculate: R = z * G
Calculate: r from R
Calculate: s = z + Hash(r||P||m) * k
Signature = (r, s)
The verification of Schnorr Signature is shown below:
Signature: (r, s)
Public Key: P
Message: m
--- the above are already given ---
Calculate: R from r
Verify: s * G
= (z + Hash(r||P||m) * k) * G
= z * G + Hash(r||P||m) * k * G
= R + Hash(r||P||m) * P
In the case when r, s, G, R, P, and m are given, we can verify the equation s * G. If it’s true, the Schnorr Signature is valid.
So what makes Schnorr Signature better than secp256k1? Well, let’s look at the main difference between the two algorithms:
Secp256k1:
s = (m + r * k) / z
Schnorr:
s = z + Hash(r||P||m) * k
As you can see, Schnorr doesn't have any divisions. This feature makes Schnorr Signatures linear, which enables batch signing, shown below:
Private Keys: k1, k2
Public Keys: P1 = k1 * G, P2 = k2 * G
Message: m
--- the above are already given ---
Aggregated Public Key: P = P1 + P1
Generate random numbers: z1, z2
Calculate: z = z1 + z1
Calculate: R = z * G
Calculate: r from R
Signature 1: s1 = z1 + Hash(r||P||m) * k1
Signature 2: s2 = z2 + Hash(r||P||m) * k2
Aggregated Signature: s = s1 + s2 = (z1 + z2) + Hash(r||P||m) * (k1 + k2)
Signature = (r, s)
Batch signing makes multi-signature verification much more efficient, as you can see below:
Signature: (r, s)
Public Key: P1, P2
Message: m
--- the above are already given ---
Calculate: R from r
Calculate: P = P1 + P2
Verify:
s * G
= (s1 + s2) * G
= ((z1 + z2) + Hash(r||P||m) * (k1 + k2)) * G
= (z1 + z2) * G + Hash(r||P||m) * (k1 + k2) * G
= z * G + Hash(r||P||m) * (P1 + P2)
= R + Hash(r||P||m) * (P1 + P2)
In the case when r, s, G, R, P, P1, P2, P, and m are given, we can verify the equation s * G. If it’s true, the Schnorr Signature is valid.
This neat property allows us to add two Schnorr Signatures to produce another valid Schnorr Signature. That's one of the reasons why Schnorr Signature is warmly welcomed when we already have secp256k1. Secp256k1 can't compress multiple signatures in batch.
Let’s summarize with the following table to show the property of Schnorr Signature:
| Private Key | Public Key | Signature | Message | Validated |
| Pair 1 | k1 | p1 | sig1 | m | Pass |
| Pair 2 | k2 | p2 | sig2 | m | Pass |
| Pair 3 | - | p1 + p2 | sig1 + sig2 | m | Pass |
The table shows that the three public key/signature pairs (Pair 1, Pair 2, Pair 3) can be validated successfully against the same message m. Again, that's the magic of Schnorr Signature's linearity property: all signatures and public keys can be thus combined into a single signature and a single key.
Hide Transaction Details in Schnorr Pubic Key
Let’s start with an analogy of a locked box:
The owner of a message put the message in a box and locked it, then gave the box to another person(s). The message inside the box is hidden from the receiver, who cannot open the lock himself/herself. But because the receiver has the box, the message inside can be revealed—but not changed—as long as the owner agrees to give out the key sometime later.
Due to the linearity of Schnorr Signature, some extra information can be embedded into the public key. This is achieved by tweaked key.
Here is the way to generate a tweaked public key (also known as Taproot output key):
Information to hide: h
Private Key: k
Taproot internal key: P = k * G
Taproot output key: P2 = P + Hash(P||h) * G
Continuing with our analogy, the Taproot output key is the locked box with the message inside. The Taproot output key and Taproot internal key are valid Schnorr public keys. It’s easy to validate the information h is embedded in P2.
Given P2, P, and h, it must satisfy:
P2 = P + Hash(P||h) * G
See more details on taproot_tweak_pubkey in Python code under the Script Path Spending section in Part 2. It makes sense that when the owner gives out the key to the receiver to reveal the message, the receiver can be sure that the message is indeed from the owner.
Remember that the Schnorr Signature can only prove that some hidden information (h) is in the Taproot output key. We can’t extract the content of the information from it. The same rule applies to the Merkle Tree which I’ll introduce in the following section.
A Schnorr public key, concealing information inside, looks the same as a normal public key. You can’t distinguish between a Taproot output key (P2) and a normal public key (P) before revealing it.
Hide Transaction Details in Merkle Tree
Merkle Tree is a tree-like structure in which every leaf (node) is labeled with the hash of a data block, and every node that is not a leaf (branch) is labeled with the hash of the labels of its child nodes. In the diagram below, L0, L1, L2, and L3 are leaves, while H, H0, H1, H00, H01, H02, and H03 are branches. The most relevant branch is the root hash on the top.
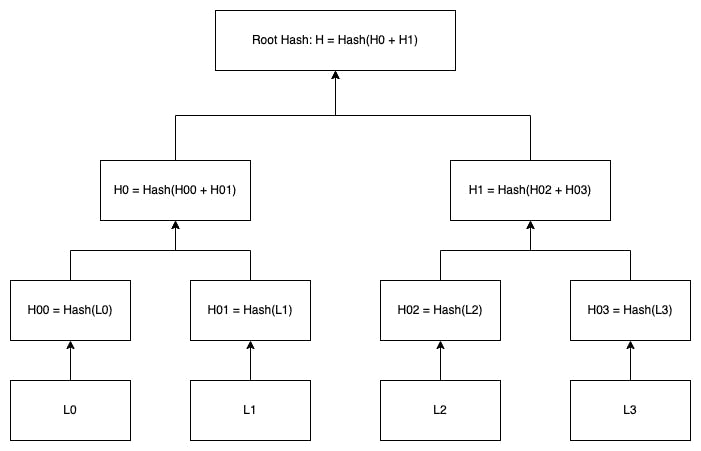Figure 1. Leaves, branches and the root in a Merkle Tree
Suppose we have a Merkle root hash, how can we prove that the data block L0 is in the Merkle Tree?
This scenario, known as a proof-of-inclusion, demonstrates that Merkle Tree is efficient for proving the existence of data. The root of this tree is just a hash that tells us nothing about the content of the tree. We can use “Merkle proof” to demonstrate whether certain content is part of this tree. For instance, if we need to prove that L0 is part of the tree, all we need to do is provide each of L0’s siblings all the way up, and recompute the tree to see if the root hash matches. The L0 and its siblings are colored in blue in the diagram below:
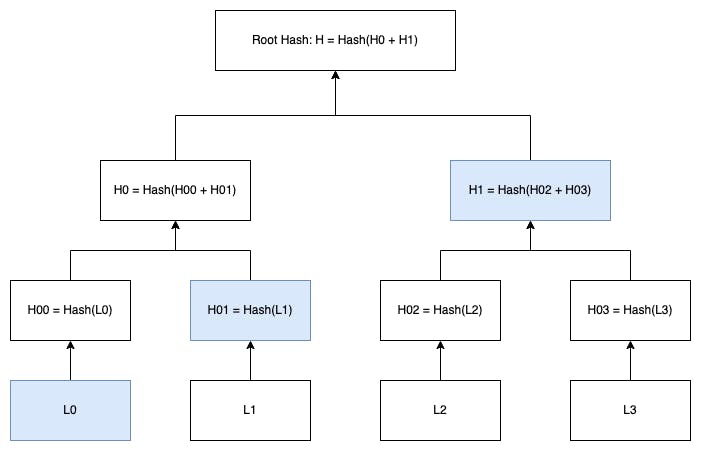Figure 2. Perform a proof-of-inclusion in Merkle Tree
With L0, H01, and H1 alone, we can recompute the original root hash. This is an efficient way to show that L0 is part of the tree without walking through the entire tree.
It’s interesting to notice that the tweaked public key can be considered as a simple Merkle Tree too, with the structure shown below. Tweaked public key has two leaves and one branch: root hash.
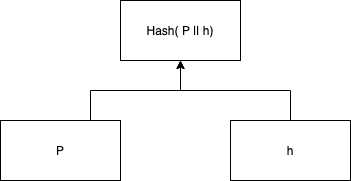Figure 3. Tweaked public key represented in the structure of Merkle Tree
In Taproot, the Merkle root hash is embedded as hidden information in Taproot output key. We will use this information (Merkle root hash) in the following part on Taproot workflow.
Taproot Workflow
We have learned that Schnorr public key and Merkle Tree both can hide transaction details. Moreover, the data blocks in the leaves of Merkle Tree are scripts. That means it’s possible for the owner to embedded many scripts in Merkle Tree. Now, it’s time to reveal the hidden information.
Assume we already have a Taproot output key (a valid Schnorr public key). The Taproot workflow consists of the following two steps:
Step 1. Reveal Merkle Tree root hash from Taproot output key by providing:
- Taproot internal key
- Taproot output key
- Merkle Tree root hash
Step 2. Prove that the script is in Merkle Tree by providing:
- Merkle Tree root hash
- Merkle proof
- Script
If all the steps can be successfully verified, we can trust that the script is embedded by the owner and run it. The returned code of the script is the final result of the unlocking process.
Like Bitcoin, CKB uses scripts as well. As CKB builders and lovers, we appreciate the beauty of Bitcoin Taproot’s design and potential, and also wonder if it’s possible to integrate Taproot into CKB. If possible, it would be a win-win: CKB may benefit from Bitcoin advancements and Bitcoin may also share the efforts of Nervos’ community.
So, in the following Part II of Enable Bitcoin Taproot on CKB, I'll explain how we integrate Taproot into CKB with a few specific examples. You will see how flexible spending can be!
✍🏻 Written by: Jiandong Xu
Posts by the same author:
You might also be interested in...
