Building a Zero-Knowledge Virtual Machine on CKB-VM for Privacy-Preserving and Secure Computing
Introduction
Zero-knowledge proofs (ZKPs) are cryptographic protocols that enable a prover to prove the truth of a statement to a verifier without revealing any additional information beyond the statement's validity. This technology has a wide range of applications, including privacy-preserving computations, authentication, and secure data sharing.
A Zero-knowledge Virtual Machine (ZK-VM) is a powerful application of ZKPs that can execute programs written in its instruction set and prove the validity of its execution to the verifier without revealing sensitive data. This makes ZK-VMs a useful tool for privacy-preserving computations and secure decentralized applications. Additionally, with ZKPs, the verifier can verify that the program was executed correctly without needing to perform the computation locally, saving significant computational resources. The ZK-VM's proof can be verified using only a small amount of computation, making it possible to perform secure computations on devices with limited processing power or in resource-constrained environments.
In this article, we will share our experience in implementing a ZK-VM prototype based on the Brainfuck language using the Halo2 library. The project is available in our repository. Our prototype enables us to validate the execution of an arbitrary BF program in the CKB-VM. Rather than focusing on cryptography theories or complex mathematical formulas, this article emphasizes an intuitive understanding of the ZK-VM and its implementation.
A BF-VM
Brainfuck (BF) is a minimalistic programming language that uses only eight commands to manipulate a tape of cells, each initially set to zero. A regular BF-VM uses a memory pointer (mp) and an instruction pointer (ip) to maintain its state. For the purpose of zero-knowledge proof, we also require a set of extra registers to be maintained. For this article, the following registers are mentioned:
a memory value register (
mv) stores the current value pointed by the memory pointer.a cycle register (
cycle) stores the current cycle of the execution
The BF language is Turing complete, meaning it can compute any computable function given enough time and memory.
The eight commands in BF are:
>Move the memory pointer to the right<Move the memory pointer to the left+Increment the value at the memory pointer-Decrement the value at the memory pointer.Output the value at the memory pointer,Input a value and store it at the memory pointer[If the value at the memory pointer is zero, jump forward to the matching]]If the value at the memory pointer is nonzero, jump back to the matching[
For example, a classic Hello, World! program in BF would look like this:
++++++++++[>+++++++>++++++++++>+++>+<<<<-]
>++.>+.+++++++..+++.>++.<<+++++++++++++++.
>.+++.------.--------.>+.>.
KZG-based Halo2
Image sourced from Twitter
Halo2 is an implementation of a zero-knowledge proving system written in Rust that utilizes advanced techniques in the field of zero-knowledge proofs. Its high-level interface for building circuits and generating proofs makes it easy to develop custom zero-knowledge proof systems in Rust. By default, Halo2 uses PLONKish arithmetization to build circuits and the Inner Product Argument (IPA) as its commitment scheme, as shown in the figure above. However, for our purposes, we opted to use the KZG variant provided by the Scroll team. The KZG commitment scheme offers superior efficiency in terms of proof size, proving time, and verification time, theoretically achieving constant verification time and proof size regardless of the input size. However, a trusted setup phase is required in order to use KZG-based pairing, where trusted parties perform a setup ceremony to generate the initial parameters for the proof generation process. It is crucial to execute this setup phase accurately and securely to prevent compromising the system's security. Despite the downside of a trusted setup, we believe the performance benefits of the KZG-based pairing outweigh this requirement.
Proving a BF Program
Our BF-VM aims to execute BF programs and generate a trace. This trace serves as input for Halo2 circuits, enabling the generation of a proof. The proof can subsequently be validated by a verifier deployed on the CKB blockchain. Additionally, Halo2 incorporates the Fiat-Shamir transformation to ensure a non-interactive protocol. To illustrate the general workflow of a ZK-VM, please refer to the following flowchart.
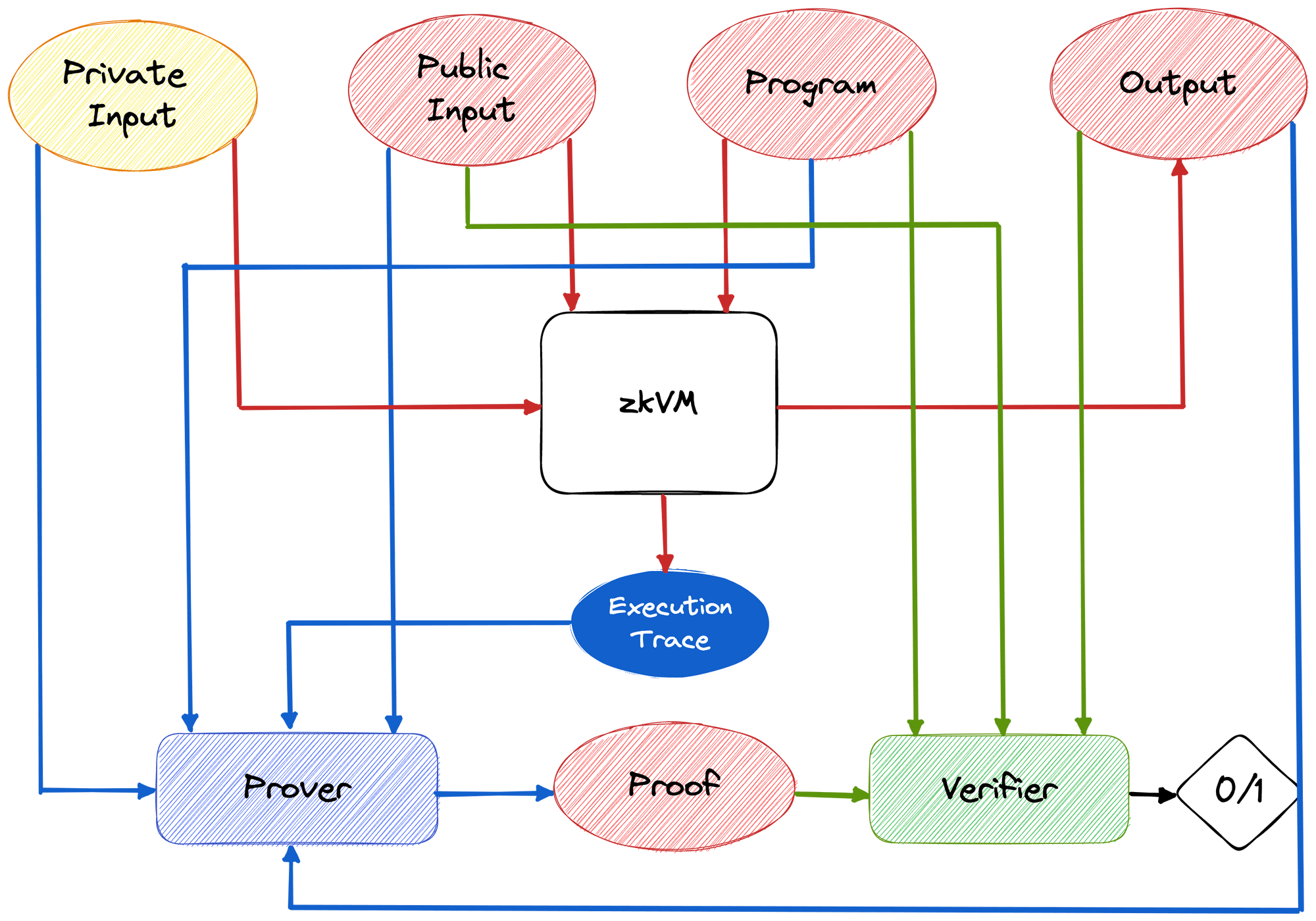
Trace
A trace consists of the history of the execution, including the state of the VM at each cycle. Specifically, our ZK-VM needs to produce the following information:
Processor table
A table that contains the register information at each cycle, sorted by cycle.
Memory table
A table that contains the same information as the processor table, but is sorted by memory pointer and then cycle.
Instruction table
A table which is the union of the program code and processor table.
Input/Output table
A table contains the program's input and output in their natural order.
Program table
A table that contains the program instructions.
Our proof system first needs to validate the correctness of each table in the trace. This can be done through the Halo2 circuit system. In the following examples, we will demonstrate a couple of proofs written in Halo2 circuits to provide a better understanding of what we are trying to prove and how we do it.
Example 1: Proving the consistency of memory pointer.
In this example, we want to prove that the states of the memory pointer in our trace are correct. This utilizes our Memory Table mentioned in the previous section. Observe that the Memory Table is sorted by the memory pointer, and the BF's semantics only allow the memory pointer to be increased or decreased by one for a single cycle. Therefore, for a valid Memory Table, we must have the following constraint satisfied:
For each row in the table, the memory pointer increases by one or zero.
We then translate this observation into constraints written in Halo2:
cs.create_gate("M0: memory pointer either increase by one or by zero", |vc|
{
// memory pointer in current cycle
let cur_mp = vc.query_advice(mp, Rotation::cur());
// memory pointer in next cycle
let next_mp = vc.query_advice(mp, Rotation::next());
// A selector to control whether a constraint should be active or not
let s_m = vc.query_selector(s_m);
// The polynomials representation of our constraint
vec![s_m * (next_mp.clone() - cur_mp.clone() - one.clone()) * (next_mp.clone() - cur_mp.clone())]
});
The s_m selector is Halo2-specific and tells the Halo2 system whether a constraint is active. Ignoring that for a moment, we can see that at the end, we formalize the constraint through a polynomial function: \((MP_{next} - MP_{cur} - 1) \times (MP_{next} - MP_{cur})\) . The polynomial evaluates to zero only when either the left part evaluates to zero or the right part evaluates to zero. In particular, the left part evaluates to zero iff the memory pointer is increased by exactly one in the next cycle. The right part evaluates to zero iff the memory state is the same in the current and next cycle. This polynomial perfectly reflects our observation at the beginning.
Example 2: Proving the execution is overflow-free
In this example, we aim to ensure that our execution is overflow-free. Since our BF-VM operates within an 8-bit domain, valid values range from \(0\) to \(255\). When we increase or decrease a value that is already at the limit, we expect it to wrap around, meaning \( 0-1 \) becomes \(255\) and \(255 + 1\) becomes \(0\).
We first validate the domain, which can be accomplished using the lookup table feature built into Halo2. A lookup table allows us to specify a range and validate that a set of values are within that range:
fn load_table(&self, layouter: &mut impl Layouter<Fr>) -> Result<(), Error> {
layouter.assign_table(
|| "load range-check table",
|mut table| {
let mut offset = 0;
for value in 0..RANGE {
table.assign_cell(|| "value", self.table, offset, || Value::known(Fr::from(value as u64)))?;
offset += 1;
}
Ok(())
},
)
}
This Rust code defines a function that loads a lookup table used to validate a range of values. The function takes a mutable reference to a Halo2 Layouter object, which is used to assign values to the lookup table. The assign_table method initializes the lookup table with a set of values within the specified range. For our cases, valid values are \(0\) to \(255\). The values are assigned to the lookup table by calling the assign_cell method on the table object, which is passed as an argument to the closure.
Then, we incorporate the lookup table into our circuits using the lookup function:
cs.lookup("Range-Check: mv are within 0-255", |vc| {
let s_lookup = vc.query_selector(s_lookup);
let mv = vc.query_advice(mv, Rotation::cur());
// lookup_table.table is our lookup table
vec![(s_lookup * mv, lookup_table.table)]
});
Here, s_lookup serves as our selector, and the final polynomial ensures that the memory value at each cycle falls within the range specified in the lookup table.
Next, we validate that the regular operations that modify the memory value are correct. In BF's instruction set, + and - increase or decrease the memory value by one, respectively. Therefore, we create a constraint in the processor table as follows:
cs.create_gate("Add and Sub operate correctly", |vc|
{
let expr_add = deselectors[ADD].clone()
* (next_mv.clone() - cur_mv.clone() - one.clone());
let expr_sub = deselectors[SUB].clone()
* (next_mv.clone() - cur_mv.clone() + one.clone());
vec![expr_add * expr_sub]
}
A deselector for op evaluates to zero iff current_instruction != op. This is particularly useful when validating each of BF's instruction semantics and only activating the correct constraint for the corresponding instruction. In other words, the deselector[ADD] evaluates to a non-zero value only when the current instruction in the instruction pointer is ADD(+). Therefore, to satisfy the constraint, the right-hand side of the polynomial must return zero. Combining these facts, the constraint we created (expr_add) for ADD operations says that (1) if the current operation is not ADD, the constraint evaluates to zero (through the deselector), and (2) if the current operation is ADD, then the difference between the memory values at the current and next cycle must be one. The constraints on the SUB operation act similarly.
Finally, to validate the wrap-around behavior, we only need to add another scenario for the ADD and SUB operations:
cs.create_gate("Add and Sub operate correctly", |vc|
{
// range_max = 255
let expr_add = deselectors[ADD].clone()
* (next_mv.clone() - cur_mv.clone() - one.clone());
* (next_mv.clone() - cur_mv.clone() + range_max.clone())
let expr_sub = deselectors[SUB].clone()
* (next_mv.clone() - cur_mv.clone() + one.clone());
* (next_mv.clone() - cur_mv.clone() - range_max.clone())
vec![expr_add * expr_sub]
}
The extra polynomial specifies that for ADD operations, it is also okay for the memory value to be decreased by \(255\) at the next cycle. This only happens when the current memory value is \(255\), and the wrap-around causes the result of \(255 + 1\) to be \(0\). A careful reader might ask whether this could also happen for other cases, such as \(102 + 255 = 357\), resulting in a false-positive. However, recall that we have a lookup table to ensure values are always within \(0\) and \(255\), hence securing our constraints.
Proving all tables refers to the same program
So far, we have demonstrated through several examples how to prove that each table within the trace is internally consistent. However, this alone does not guarantee a valid trace. For instance, a malicious prover could provide a program table from a "Hello World" program and a memory table from a Fibonacci program, both of which can be proven to be internally correct but together do not constitute a valid trace. Therefore, we must prove that all of the tables point to the same program, i.e. all tables are connected.
This can be achieved through two powerful functions: a permutation running product (PRP), which proves that two tables are permutations of each other, and a running evaluation (RS), which proves that two tables are identical. We will not delve into the details of how to write these constraints in Halo2 here, but the basic idea is as follows:
The process and memory tables contain the same data but are sorted differently, so a PRP check can be used to prove that these two tables are permutations of each other.
The instruction table contains the static program and runtime execution history. Specifically, the part that contains the execution history must be identical to the processor table, which can be proven through an RS check. Similarly, the part that contains the static program must be identical to the program table. We can extract the static program and runtime execution part separately by using polynomial constraints.
The input table contains all the user inputs. The program must then read these inputs, which can be found in the rows of the processor table where the instruction pointer contains
GET_CHAR(,). By carefully extracting these parts using the deselector, they must be identical to the input table through RS check. Similarly, we can use the deselector to extract the part withPUT_CHAR(.), which must be identical to the output table.
Final Step
Before we can claim victory, there is one more step we need to take. While we have already proven, from the prover's perspective, that we hold a valid trace with consistent internal states that all refer to the same program, we still need to ensure that the trace we have proven is the one that the user expects. Note all the proofs so-far are zero-knowledge, meaning only the validity of the statement is proven and nothing else about our trace is revealed. Hence we cannot guarantee that a malicious prover won't provide a valid trace of a malicious program while the user expects a trace from a "Hello World" program.
To achieve this, we can utilize the instance column in Halo2. An instance column allows the verifier to provide some public data that can be used for the proof. For our use case, by making the program code and program input into an instance column, and writing the circuits so that the program table and input table are extracted from those public data, we eliminate the possibility for a malicious prover to modify what is being proven. This is because public data must be provided by the verifier, ensuring that the proof is based on the expected program and input.
Verifying a Concrete Program
In this section, we provide a hands-on demonstration of how to use our toolchain to verify a simple BF program.
For our example, we use a basic echo program written in the BF language. This program takes user input that ends with ^] (ASCII code 29) and prints it to standard output. While the program seems simple, the trace it produces is quite long due to the low-level nature of the BF language. For example, when echoing input like "Hello World!", the resulting trace has \(2^{17}\) rows.
To begin, we clone and build the project:
git clone <https://github.com/cryptape/ckb-bf-zkvm>
cd ckb-bf-zkvm && make install && make all
After that, we proceed with running the prover to execute the echo program. This step is conducted off-the-chain and involves invoking our BF-VM to execute the program, retrieve the trace, and generate the corresponding proof. This step is also the most expensive of all.
RUST_LOG=info cargo run --release --package ckb_bf_prover -- res/echo.bf 'hello world!^]'
Behind the scene, the prover invokes the BF-VM to execute the program and obtain the trace:
let mut f = std::fs::File::open(&args[1])?;
let mut c: Vec<u8> = Vec::new();
f.read_to_end(&mut c)?;
let mut i = Interpreter::new();
let code = code::compile(c.clone());
i.set_input(code::easygen(&args[2]));
i.set_code(code.clone());
i.run();
let trace = i.matrix;
For this prototype, we will skip the trusted setup and use a dummy parameter instead:
// where k is the exponent of the size of the trace (2^k)
let s = Fr::from_u128(GOD_PRIVATE_KEY);
let general_params = ParamsKZG::<Bn256>::unsafe_setup_with_s(k, s);
From the parameter, we can generate the corresponding proving key for the prover:
let pk = keygen_pk(&general_params, vk, &circuit).expect("keygen_pk");
Next, we generate the transcript and create the proof. A transcript is an abstract object that holds the proof we will later send to the verifier:
let mut transcript = Blake2bWrite::<_, G1Affine, Challenge255<_>>::init(vec![]);
create_proof::<
KZGCommitmentScheme<Bn256>,
ProverSHPLONK<'_, Bn256>,
Challenge255<G1Affine>,
XorShiftRng,
Blake2bWrite<Vec<u8>, G1Affine, Challenge255<G1Affine>>,
MyCircuit<Fr, DOMAIN>,
>(
&general_params,
&pk,
&[circuit],
&[&public_inputs],
rng,
&mut transcript,
)
.expect("create_proof");
Finally, we serialize the program, input, proof, parameter, and verifying key into a dummy transaction file:
build_ckb_tx(
&proof[..],
&verifier_params_buf[..],
&vk_buf[..],
&code_u8[..],
&raw_input[..],
"target/riscv64imac-unknown-none-elf/release/ckb_bf_verifier",
);
We then verify the transaction file using the verifier:
ckb-debugger --tx-file res/tx.json --cell-index 0 --cell-type input --script-group-type lock --max-cycles 20000000000
Behind the scene, the verifier deserializes the proof object and verifies the proof using the Halo2 library:
let mut verifier_transcript = Blake2bRead::<_, G1Affine, Challenge255<_>>::init(&proof_buffer[..proof_len]);
let strategy = SingleStrategy::new(&verifier_params);
// vk is deseralized from the transcation. instances are the public input
let res = verify_proof::<
KZGCommitmentScheme<Bn256>,
VerifierSHPLONK<'_, Bn256>,
Challenge255<G1Affine>,
Blake2bRead<&[u8], G1Affine, Challenge255<G1Affine>>,
SingleStrategy<'_, Bn256>,
>(&verifier_params, &vk, strategy, &[&instances], &mut verifier_transcript);
Tuning Halo2 for CKB-VM
While we have a prover and verifier that can handle any BF program and return a proof using Halo2, there are practical issues with the KZG-based commitment scheme's supposed constant verification time and proof size. In the following few paragraphs, we explain how we tune the Halo2 library for CKB-VM for optimal performance.
Reducing VK Size and Memory Consumption
The size of the verification key (VK), which is part of the proof, is largely determined by the number of selectors used in the circuits. During serialization, these selectors are written into the VK, resulting in a large amount of data for longer traces. Although selectors are binary values and can be compressed into a bit format, the amount of data is still substantial. Halo2 did implement a compression algorithm to compress selectors into SelectorAssignment objects, but the Halo2 team did not provide a serialization method for it, leading to the need for re-computation on the verifier's side. This approach increases both the VK size and the memory consumption of the verifier, since the compression algorithm is quite memory-intensive. In our fork version of Halo2, we have provided a complete serialization of SelectorAssignment. This means we perform the compression algorithm only once on the prover's side, eliminating the need for re-computation on the verifier's side. As a result, we have a constant 2Kb of VK size and have avoided potential out-of-memory issues on the CKB-VM.
Improving Verification Time
In previous sections, we mentioned that the verifier must provide the program code and input as part of the public data to validate that the correct program has been proven by the prover. However, public data comes with a cost. Since the verifier is responsible for providing the public data, it must perform the necessary commitment scheme on those data instead of leaving it to the prover. This means that the larger the public data, the more computation is required for the verifier. However, there is a trick that we can use to minimize this extra cost. Instead of providing the entire program and input as public data, we can only provide a hash value of those data. For our implementation, we have chosen the Poseidon hash, which is an efficient curve-friendly hash function. A user who wants to validate an execution trace on the CKB-VM must provide the Poseidon hash of the public input. This means that the size of the public input is always constant. On the prover side, we use the hash gadget built inside the Halo2 library, which computes the Poseidon hash of a set of data and proves the hash computation's correctness. We use this gadget to compute a hash value from the program table and input table. Finally, we add an extra constraint in the circuit stating that the proof can only be validated when the hash value provided in the public data is consistent with the value computed from the program and input table, meaning the correct program has been proven.
This approach adds extra computation steps for the prover, which is not critical as the prover is usually assumed to run on a more computationally powerful machine. The important thing is that the verifier can now easily compute its public data and complete the proof. From our experiments, the cycle cost on the CKB-VM drops from 170M to 130M when using hash value as the public data.
Conclusion
Halo2 is a versatile framework that provides a robust set of tools for developing zero-knowledge proof systems for various use cases. By incorporating a simple ZK-VM with CKB-VM using Halo2, we have shown how this framework can be leveraged to extend CKB-VM's applications. As the field of zero-knowledge proofs continues to evolve, we anticipate more advanced techniques and frameworks emerging to support more complex proof systems, opening up new opportunities for secure and private computation.
✍🏻 by Xiaowen Hu, Jiandong Xu, Biao Yi, Wanbiao Ye
You may also be interested in:

